領域概要
研究領域の概要
エネルギーの生成と消費の釣り合いは、近い将来大きな問題を抱えることが予想されています。IT分野を中心としてエネルギー消費量は指数的な増大を見せている一方、エネルギーの生成原理は蒸気機関の時代から本質的に変化していません。本研究領域ではこの問題に対し、理論と実験の両面から、量子効果を用いた根本的なブレイクスルーを目指しています。具体的には、量子計算機が古典計算機と比べて圧倒的な高効率を示す「量子優位性」が、エンジンをはじめとしたエネルギーデバイスでも実現することを理論的に確立し、さらに実験室レベルで実証していきます。
目的
量子効果を用いた超効率エンジンの理論的・実験的ブレイクスルー
本研究領域では、近年の熱力学理論を抜本的に発展させ、量子効果によるエネルギー生成・利用の超効率化を理論的・実験的に研究します。これまでも量子効果は多くのデバイスの性能を向上させてきましたが、それらは通信・計算・センシングなど、情報関連の技術に限定されていました。しかしエネルギー問題に代表されるように、現実の世界は情報技術と直接的な結びつきのない問題を数多く抱えています。そうした問題の多くは、量子熱力学的な枠組みでとらえられる構造を持っており、エネルギー問題と類似したアプローチを適用できると期待できます。本領域の究極的な目標は、本領域のエネルギー問題に対する量子的なアプローチを発展させ、情報以外の問題を広く量子で解決する処方箋を与えることにあります。
計画目標と班構成
本領域の具体的な目標は以下の通りです。
- エネルギーが携わる多様なデバイス・対象における量子強化の普遍的手法の確立
- 飛躍的性能強化を示すTF モデル熱機関の実験による実現
- 古典非マルコフ熱機関によるTF モデル熱機関の飛躍的性能の再現可能性の検証
- 最適性に基づく量子強化の改善と、達成可能な限界の探求
これらの目標を達成するために、本領域ではA01からA04まで4つの研究班を立ち上げました。これに総括班を加えた5グループが、本領域の構成班です。それらの間の構造は以下の図のようになります。
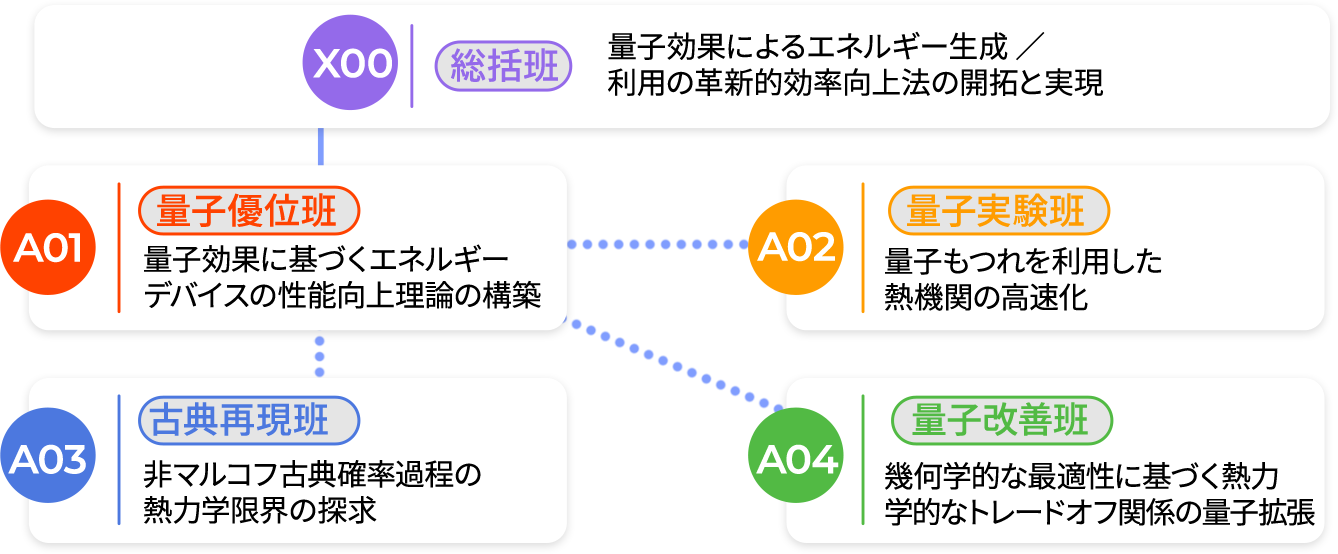
X00:総括班
領域代表:田島 裕康
共同研究促進・広報、情報発信・国際活動を実行し、研究領域の推進を加速させます。
A01:量子優位班
量子効果に基づくエネルギーデバイスの性能向上理論の構築
近年、量子力学の性質を用いて、計算やセンシングなどの様々なタスクをオーダーレベルで性能向上させることが実現されつつあります。こうした発展の中、本A01班の田島・布能によって、量子効果を用いることで、熱機関などのエネルギーデバイスを線形オーダーで性能向上し、古典限界を突破できるという理論が提案されました。上記の結果はエネルギーデバイスに対する「量子優位性」としての初めての例ですが、その全貌はより高次オーダーの性能向上の可能性を含め全くの未開拓です。そこで本A01班では、この未踏の分野に挑み、量子効果によるエネルギーデバイスの線形オーダーを超えた性能向上に関する一般論を求めことを目指しています。また、このような性能向上を活用し、理想的な熱・仕事変換効率と高出力を合わせ持つ熱機関を実験で実装するための理論提案を行うことで、エネルギーサイエンスにおけるブレイクスルーを引き起こすことを目指しています。
A02:量子実現班
量子もつれを利用した熱機関の高速化
本A02班では、超伝導量子回路によって熱機関を構成し、古典力学に従う従来の熱機関に対して優位性を持つ量子熱機関の実証を目指しています。超伝導量子回路は、高精度に制御・測定が可能な量子系として、情報熱力学のプラットフォームとして着目されてきました。本A02班では、超伝導量子回路のこの特徴を活かし、その集積性と高精度制御技術をさらに発展させることで、複数の量子ビットが協調して動作する量子熱機関を構成できると考えています。これらの研究を通し、熱機関における量子優位性を評価するとともに、全結合量子回路を用いた量子制御技術を開拓していくことが、本班の目標です。
A03:古典再現班
非マルコフ古典確率過程の熱力学限界の探求
古典非マルコフ過程においては、班代表の金澤が発展させてきた一般的な解析手法が確立されつつあります。本A03班ではこれを拡張し、古典非マルコフ過程に従う熱機関の性能限界を調べる理論を確立することを目指します。特に、量子重ね合わせによって起こる量子協同現象(超放射・超吸収)をどの程度非マルコフ効果によって再現できるかを調べていきます。同時に、量子優位班と協力して非マルコフ過程における量子熱力学の枠組みも整備します。
A04:量子改善班
幾何学的な最適性に基づく熱力学的なトレードオフ関係の量子拡張
本A04班の代表である伊藤は、最適輸送・情報幾何などの幾何学の手法を用いて、熱力学的トレードオフ関係の最適化を行ってきました。実際、古典系において最適性に基づいた熱力学的トレードオフ関係式は伊藤らによって導出されたものです。TF 理論が与える不等式は量子系における熱力学的トレードオフ関係式と呼べる結果なので、伊藤の熱力学的トレードオフ関係を量子拡張するとともに、量子系での幾何学的な最適化手法を開発します。また開発した手法を援用することで、TF 理論およびその発展形の改善/最適化を行うことを目指していきます。

